动态规划复习笔记

0.前言

本蒟蒻学习完动态规划后仍然有些懵，于是就有了这篇复习笔记，希望可以通过这种方式使我掌握动态规划。

欢迎各位大佬挑错。

什么是动态规划？

把一个大问题转换成若干个规模较小的同类型问题（子问题），当我们求出这些子问题的答案，大问题便可以求出。

在求解这些小问题的过程中，需要把重复计算的答案记录到数组中，如果遇到相同的小问题，便直接查询出结果。

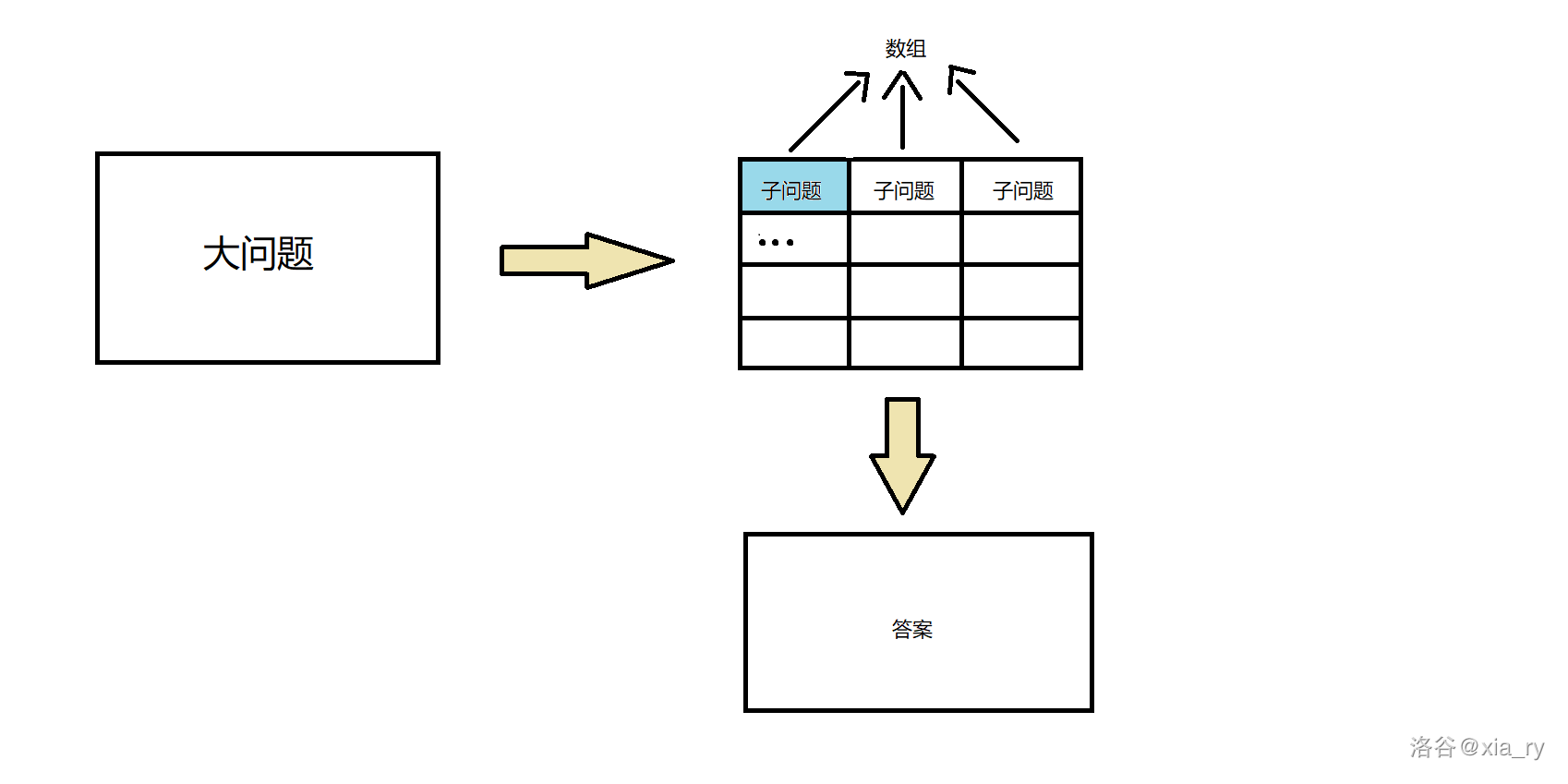
我们来看一下官方的说法：

其中，各阶段之间的关系，指的就是状态转移方程。那么状态转移方程是什么呢？其实就是大问题与子问题之间的关系。

举个例子：假如我们有1元、5元和11元的纸币若干张，怎样才能使用尽可能少的纸币凑15元呢？

按照正常的思路，我们会尽可能的多拿面值大的：

$11×1 + 1×4 = 15$ ，一共5张。

但是这是最优的吗？

可以发现
$3×5 = 15$ ，一共3张，按常规思路来，并不是最优的。

我们不妨倒推回去 : 凑成15，有三种情况：

以此类推，我们可以发现第二种，取5所需的纸币是最少的。

我们用 $f(n)$ 来表示凑出n元所需的纸币数：

要想求 $f(n)$ ，只需要知道 $f(n-1),f(n-5),f(n-11)$ 三者中的最小值，也就是：

这就是一个动态转移方程

还有一些其他的概念：

要求出 $f(15)$ ，只需要知道 $f(14),f(10),f(4)$ 的值，而 $f(14),f(10),f(4)$ 是如何算出来的，对之后的问题没有影响。
将来的和之前的没有关系，就是无后效性

我们只要知道子问题 $f(14)、f(10)、f(4)$ 的最优解，就可以得出大问题 $f(15)$ 的最优解。

大问题的最优解可以由小问题的最优解推出

这种性质就叫“最优子结构性质”。